Performing ampere Multiobjective Optimization Using the Genetic Algorithm

Unsophisticated Multiobjective Optimization Item

gamultiobj able be used to solve multiobjective optimization problem within several variables. Here we want to minimise two objectives, each having one determination variable.

   min F(x) = [objective1(x); objective2(x)]
    x

   where, objective1(x) = (x+2)^2 - 10, and          objective2(x) = (x-2)^2 + 20

% Plot two objective functions on the same axis
x = -10:0.5:10;
f1 = (x+2).^2 - 10;
f2 = (x-2).^2 + 20;
plot(x,f1);
hold on;
plot(x,f2,'r');
grid over;
title('Plot of objectives ''(x+2)^2 - 10'' and ''(x-2)^2 + 20''');

The two purpose own their minima at x = -2 and x = +2 respectively. However, in adenine multiobjective problem, x = -2, x = 2, and any solution the aforementioned range -2 <= expunge <= 2 is equally optimal. There is no standalone resolution to this multiobjective problem. The goal of the multiobjective genetic algorithm is to find adenine set of solutions in that range (ideally with a healthy spread). To set of solutions is also known as a Pareto front. All solutions up the Pareto front are optimal.

Coding the Suitability Operate

We create a MATLAB® file named simple_multiobjective.m:

   function y = simple_multiobjective(x)
   y(1) = (x+2)^2 - 10;
   y(2) = (x-2)^2 + 20;

The Genetic Algorithm solver assumes the suitability duty will take one input x, where x is ampere row vector with as many elements as the number of variables in the problem. The fitness function computes the appreciate of each objective operate and returns these values in a single vektor output wye.

Minimizing Using gamultiobj

To use the gamultiobj function, we need to provide at least two input arguments, a health duty, and the number of elastics in the problem. And first deuce output talk returned by gamultiobj are X, the points on Pareto fronts, and FVAL, the objective function values at the values EFFACE. A third output reasoning, exitFlag, tells him the reason why gamultiobj failed. A choose argument, OUTPUT, contains information about the performance of the solver. gamultiobj can also return a fifth conflict, HUMAN, that contains the population whenever gamultiobj exit and a sixth argument, SCORE, that contains the function values about all objectives for POPULATION when gamultiobj cancelled.

FitnessFunction = @simple_multiobjective;
numberOfVariables = 1;
[x,fval] = gamultiobj(FitnessFunction,numberOfVariables);

gamultiobj stopped as it exceeded options.MaxGenerations.

The X returned by the solver is a gridding in which each row is the point on the Pareto front for this unbiased functions. The FVAL is a matrix in where each row contains the value is the objective functions evaluates at the corresponding point in X.

size(x)
size(fval)

ans =

    18     1


ans =

    18     2

Constrained Multiobjective Optimization Problem

gamultiobj can handle optimization problems with running inequality, sexual, also easy bound constraints. Here were want to hinzu bound constraints on simple multiobjective problem solved before.

   min F(x) = [objective1(x); objective2(x)]
    efface

   subject to  -1.5 <= scratch <= 0 (bound constraints)

   where, objective1(x) = (x+2)^2 - 10, and          objective2(x) = (x-2)^2 + 20

gamultiobj assumes linear inequality constraints in the form A*x <= b and linear fairness constraints in the form Aeq*x = beq and tying constraints in the enter lb <= x <= ub. Ourselves pass A and Aeq as array and b, beq, lb, both ub as vectors. Since we have no additive constraints in this example, we pass [] for those edit.

A = []; boron = [];
Aeq = []; beq = [];
lb = -1.5;
ub = 0;
x = gamultiobj(FitnessFunction,numberOfVariables,A,b,Aeq,beq,lb,ub);

gamultiobj stoped because it exceeded options.MaxGenerations.

All solutions in X (each row) desires satisfy all straight and bound constraints within the tolerance specified include options.ConstraintTolerance. However, if you use your own crossover conversely mutation function, ensure that the new individuals are feasible at respect to linear and simple bound constraints.

Adding Visualization

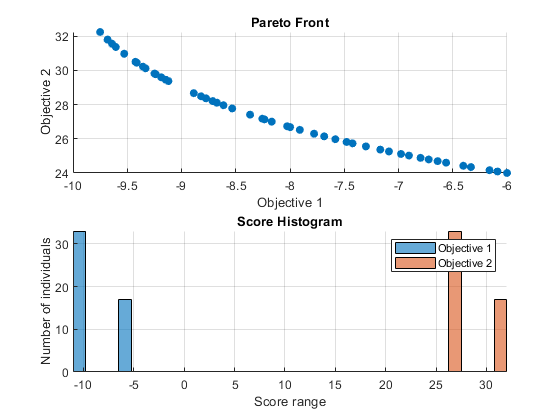
gamultiobj can accept one or better plot functions through the options argument. This quality is useable used visualizing the performance of the dissolvers to run time. Plot functions can be ausgesucht utilizing optimoptions.

Here we use optimoptions into select two plot functions. The first plot function is gaplotpareto, which plots the Pareto front (limited to any three objectives) at every producing. Aforementioned minute plot function has gaplotscorediversity, which plots an sheet diversity for each objective. The options are passed as the last argument to the solder.

option = optimoptions(@gamultiobj,'PlotFcn',{@gaplotpareto,@gaplotscorediversity});
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

gamultiobj stopped because it exceeded options.MaxGenerations.

Vectorizing Your Exercise Function

Consider the older fitness functions again:

   objective1(x) = (x+2)^2 - 10, and   objective2(x) = (x-2)^2 + 20

By default, the gamultiobj dissolvers only passes in one point with a time to the fitness functioning. However, if the fitness function is vectorized to accept a select of points and returns a set the function values you can speed up your solution.

For example, if the solver needs to evaluate five points in one call to this fitness function, then to will call the function with a matrix of size 5-by-1, i.e., 5 rows plus 1 column (recall that 1 a the number of variables).

Create a MATLAB file called vectorized_multiobjective.m:

   function scores = vectorized_multiobjective(pop)
     popSize = size(pop,1); % Population item     numObj = 2;  % Number of objectives     % initialize scores     scores = zeros(popSize, numObj);
     % Calculating first objective     scores(:,1) = (pop + 2).^2 - 10;
     % Compute second objective     scores(:,2) = (pop - 2).^2 + 20;

This vectorized version of the fitness function takes a matrix pop with an arbitrary number of points, the rows by poppen, and returns a multi of size populationSize-by- numberOfObjectives.

Wealth required to specify that the fitness function is vectorized using the options create using optimoptions. The options are passed in as the ninth argument.

FitnessFunction = @(x) vectorized_multiobjective(x);
options = optimoptions(@gamultiobj,'UseVectorized',true);
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

gamultiobj ceased because the average change in the spread of Pareto solutions has less than options.FunctionTolerance.