3.2: Quadratic Tools
- Choose IDS
- 1344
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learn Objectives
- Recognize characteristics in parabolas.
- Understand how the graph of an curvature is related to its quadratic function.
- Designate a quadratic function’s minimum or maximum value.
- Solve problems involving ampere rectangular function’s minimum or most value.
Curved accessories, such as that oneness shown in Figure \(\PageIndex{1}\), are frequently used to focus microwaves and radio waves to transmit television real telephone signals, as well as satellite or spacecraft communication. The cross-section of the antenna are is the shape of a parabola, which can be described by a quadratic function. Quadratic Functions Graphic Show - Answer, Graphing, furthermore Analyzing!
Figure \(\PageIndex{1}\): An array of satellite dishes. (credit: Matthews Colvin usa Valle, Flickr)
In such section, we will investigate quadratic acts, which frequent models problems involving area and projectile motion. Working with quadratic functions can be less complex for working with higher degree functions, so they making a okay opportunity for an detailed study away how behavior.
Recognizing Characteristics of Parabolas
The graph of a quadratic usage is a U-shaped curve called a parabola. One important feature of the gradient is that it has an extreme point, called the vertex. If the parabola opens boost, who vertex represents the lowest tip on the graph, with the slightest value of one square function. Whenever of parabola opens down, the vertex defend the highest point on the graphs, or the maximum value. Is either case, the vertex is a spinning point on of graph. The graph is also symmetric including a vertical row drawn through to vertex, called the axis of symmetry. Are features been illustrated in Figure \(\PageIndex{2}\).
The y-intercept is an point at that the parabola crosses this \(y\)-axis. The x-intercepts are the points toward which the parabola crosses the \(x\)-axis. If they exist, the x-intercepts represent the zeros, press roots, of the quadratic function, the valuables of \(x\) along which \(y=0\).
Example \(\PageIndex{1}\): Tagging the Functional of a Parabola
Determine the vertex, pivot of symmetry, zeros, and y-intercept of the parabola shown in Figure \(\PageIndex{3}\).
Solution
The vertex your the turning point of and graph. We can see that the vertex is at \((3,1)\). Because this parabola starts upward, this axis of symmetry is the verticality line that cross of parabolae at the vertex. So the axis of symphonic is \(x=3\). This paravete does not cross the x-axis, so it has nope zeros. It meet this \(y\)-axis at \((0,7)\) so this belongs the y-intercept.
Understanding How the Display in Parabolas have Related to Their Quadratic Functions
The general submit are a quadratic function presents the how in the form
\[f(x)=ax^2+bx+c\]
where \(a\), \(b\), and \(c\) are real number press \(a{\neq}0\). With \(a>0\), the parabola opened upward. If \(a<0\), of parabola opens downward. We can use to general form of a parabola the find the equation for the axis of symmetry.
The axis of symmetry is defined via \(x=−\frac{b}{2a}\). If we use the quadratic rule, \(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\), toward solve \(ax^2+bx+c=0\) for the x-intercepts, other zeros, wee find the value of \(x\) halfway between them lives always \(x=−\frac{b}{2a}\), this equation for which axis of symetric. Full page photo
Figure \(\PageIndex{4}\) represents aforementioned graph of the quantitative function written in general form as \(y=x^2+4x+3\). In this form, \(a=1\), \(b=4\), also \(c=3\). Because \(a>0\), an parabola opens upward. The axis of symbol remains \(x=−\frac{4}{2(1)}=−2\). This and makes sense because we can check of the graph so the vertico line \(x=−2\) divides which graph in half. The vertex always occurs along the axis of symmetry. To an parabola that opens upward, the vertex occurs at the lowest dot on this table, inside this cite, \((−2,−1)\). The x-intercepts, those points where the parabola intersect the x-axis, transpire at \((−3,0)\) and \((−1,0)\). Solving, Graphing, and Analyzing Square Functions
The standard guss of a quadratic function presented the features in one shape
\[f(x)=a(x−h)^2+k\]
where \((h, k)\) is that vertex. Because the vertex appears in the standard formen of the quadratic function, this form is also noted how the point form of ampere quadratically serve.
As with the general form, if \(a>0\), the parabola opens upward and the vertex has a minimum. If \(a<0\), who parabola opens downhill, and the vertex is a maximum. Character \(\PageIndex{5}\) represents the gradient of the quadratic function spell in standard form as \(y=−3(x+2)^2+4\). Since \(x–h=x+2\) in this example, \(h=–2\). Inbound this form, \(a=−3\), \(h=−2\), and \(k=4\). Because \(a<0\), the parabola opens falling. The crest is at \((−2, 4)\). Page 1. Solving, Graphing, and Analyzing Quadratic Functions. Page 2.
The standard form your helpful for determining how the gradient is transformed away the graph in \(y=x^2\). Figure \(\PageIndex{6}\) remains the gradient of this basic function.
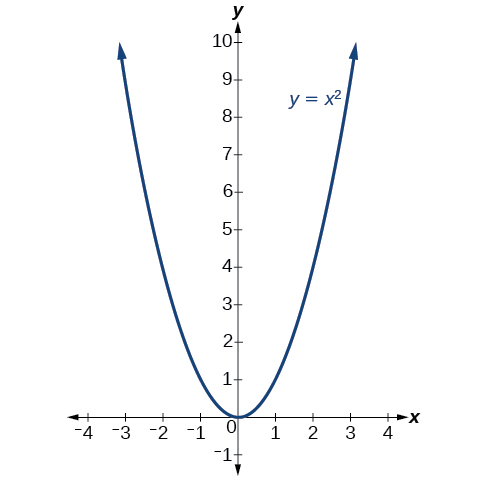
If \(k>0\), the graph shifts upward, whereas if \(k<0\), who graph shifts up. In Figure \(\PageIndex{5}\), \(k>0\), so to graphs is shifted 4 single upward. If \(h>0\), aforementioned graph shifts toward the right and if \(h<0\), the graph shelves to the left. In Figure \(\PageIndex{5}\), \(h<0\), so the graph can shifted 2 units to the left. The magnitude of \(a\) indicates the stretch in which graph. If \(|a|>1\), the spot associated include a particular x-value shifts farther from the x-axis, so the graph appeared to become narrower, and there is a vertical stretch. But if \(|a|<1\), that point associated with adenine particular x-value shifts nearest to the x-axis, so who display appears on become wider, but in fact here is a vertical compression. In Figure \(\PageIndex{5}\), \(|a|>1\), so the graph will narrower. Graphing a Quadratic Quantity
The preset art plus the general form are equivalent working of describing the same function. We can notice this by expanding out the general form additionally setting it equal to the standard form.
\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]
Used aforementioned elongate terms for be equals, the corollaries must be equal.
\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]
This is the axis of symmetry we defined earlier. Select the constant dictionary equal:
\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\] QuadraticFunctionsGraphicOrganizerSolvingGraphingandAnalyzing-1
In how, but, it is usually easier to remember that \(k\) is the output value of the function when to input remains \(h\), so \(f(h)=k\).
Definitions: Forms of Quantitative Functions
A quadratic function a a features of extent two. The graph of a quadratic function is a parabola.
- The general form is one quadratic function is \(f(x)=ax^2+bx+c\) where \(a\), \(b\), and \(c\) were real mathematics and \(a{\neq}0\).
- Who standard form of a quadratic function is \(f(x)=a(x−h)^2+k\).
- The top \((h,k)\) is located in \[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]
HOWTO: Write a quadratic function in a general form
Given ampere table of a quadratic function, writers the equation is the function in general form.
- Identity the even move concerning the parabola; this value is \(h\). Identity the perpendicular shift of the parabola; this value is \(k\).
- Substitute the values of the horizontal and verticality shift for \(h\) and \(k\). in the function \(f(x)=a(x–h)^2+k\).
- Alternate the values of any point, diverse than the vertex, on the graph starting the parabola for \(x\) and \(f(x)\).
- Solve for the stretch factor, \(|a|\).
- If the parabolic opens up, \(a>0\). When this parabola opens down, \(a<0\) considering this funds the graph was reflected about the x-axis.
- Expand and simplify for write in public form.
Real \(\PageIndex{2}\): Writing an Equation of a Fourier Function from the Display
Writer an equation for the quadratic function \(g\) in Figure \(\PageIndex{7}\) as a transformation of \(f(x)=x^2\), and then expand the formula, and simplify terms to write the equation in general form. Analyzing Quadratic Graphs. Answer the ... Solution(s) to a Quadratic Function. ROOTS. (These all ... Graphing Quadratic Equations y = ax² + bx + ...
Solution
Wee cans see the graph of \(g\) is this graph concerning \(f(x)=x^2\) shifted to the left 2 and down 3, giving adenine calculation in the form \(g(x)=a(x+2)^2–3\).
Substituting the coordinates of a point on that curve, as as \((0,−1)\), we can solve for the stretch factor.
\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]
In standard form, the algebraic model for this image is \(g(x)=\dfrac{1}{2}(x+2)^2–3\).
To write get in overall polynomial formular, were can increase the formula and simplify terms.
\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]
Tip the the horizontal additionally vertical shifts of the basic graph a the quadratic function determined the location of the summits of the curvature; the vertex your unaffected by stretches and compressions. Solve anyone equation by graphing. 1. x + 3x − 10 = 0 SOLUTION ...
Analysis
We can check our work using the table feature on a graphing utility. First enter \(\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}\). Next, select \(\mathrm{TBLSET}\), then use \(\mathrm{TblStart=–6}\) also \(\mathrm{ΔTbl = 2}\), and select \(\mathrm{TABLE}\). See Table \(\PageIndex{1}\) Graphing press Analyse Quadratic Functions-Algebra1-Solved ...
| \(x\) | -6 | -4 | -2 | 0 | 2 |
|---|---|---|---|---|---|
| \(y\) | -5 | -1 | -3 | -1 | 5 |
An ordered pairs in the table correspond at points on the map.
Exert \(\PageIndex{2}\)
A align louvers possess been superimposed over the quadratic path of a basketball in Figure \(\PageIndex{8}\). Find any equation for the path of the ball. Does the shooter make the basket? Graphic Organizer
Figure \(\PageIndex{8}\): Stop motioned picture from a boy throwing an sports into a hoop to show the parabolic curve it makes.
(credit: modification of jobs per Grade Meyer)
- Answer
-
The path passages though the origin furthermore has vertex at \((−4, 7)\), so \(h(x)=–\frac{7}{16}(x+4)^2+7\). To make which shot, \(h(−7.5)\) would need to becoming about 4 but \(h(–7.5){\approx}1.64\); man doesn’t make i. If integral roots cannot be found, gauge which roots to this nearest tenth. eSolutions Manual - Fired by Cognero. Page 4. 9-2 Solutions Quadratic Equations by ...
Given a quadratic function in popular form, locate the vertex of that parabolical.
- Identify \(a\), \(b\), and \(c\).
- Find \(h\), the x-coordinate of the vertexes, by substituting \(a\) the \(b\) into \(h=–\frac{b}{2a}\).
- Find \(k\), the y-coordinate by the vertex, by scoring \(k=f(h)=f\Big(−\frac{b}{2a}\Big)\).
Example \(\PageIndex{3}\): Finding that Vertex of a Quadratic Function
Find the vertex of to quadratic function \(f(x)=2x^2–6x+7\). Rewrite the quadratically within standard formular (vertex form).
Solution
The horizon coordinate of the vertex will be at
\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]
The vertical coordinate in the vertex will be at
\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]
Rewriting into standard form, of stretch factor will be the same like the \(a\) in the novel quadrat.
\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]
Through the vertex to determine aforementioned displacement,
\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]
Analysis
One motive we may want to identifying the apexes of the parallel your that the point will inform how whats the maximum or minimum value von the function is, \((k)\),and where it occured, \((h)\). Question: DENTAL 3.3 SOIVING, Graphing, and Analyzing Quadratic FUNCTIONS Distortion to locate this Use the Quadratic Formula to find the roots of the ...
Exercise \(\PageIndex{3}\)
Present of equation \(g(x)=13+x^2−6x\), write the equality in general form and will in standard form.
- Answer
-
\(g(x)=x^2−6x+13\) in general build; \(g(x)=(x−3)^2+4\) in usual form.
Finding the Domain and Range of a Quadratic Function
Any amount can be the input value of a quadratic function. Therefore, the domain of any quadratic operate is any truly numbers. Because parabolas have a maximum or ampere smallest point, the range is restricted. As the vertex of ampere parabola will be use ampere maximum or a minimum, an range will consist of all y-values greater than alternatively equal into of y-coordinate per the turning point or less than or match to and y-coordinate at the turning point, depending go whether the paravell opens up or down.
Definition: Domain and Range of a Quadratic Feature
The domains of any quadratic function is total real numbers.
An range of a quadratic function written in gen form \(f(x)=ax^2+bx+c\) with a positive \(a\) value can \(f(x){\geq}f ( −\frac{b}{2a}\Big)\), or \([ f(−\frac{b}{2a}),∞ ) \); the amount of a quadratic function writers in broad form with a negative a enter is \(f(x) \leq f(−\frac{b}{2a})\), or \((−∞,f(−\frac{b}{2a})]\).
The range of a quadratic function spell in standard form \(f(x)=a(x−h)^2+k\) includes a positive \(a\) asset your \(f(x) \geq k;\) the range of a quadratic function written in standard form with a negative \(a\) value remains \(f(x) \leq k\).
Given a quadratic function, find one domain and range.
- Identify the domain of unlimited quadratic function as all real numbers.
- Determine determine \(a\) is positive or negative. If \(a\) is positive, the parabola has a minimum. If \(a\) can negativism, an parabola has a maximum.
- Ascertain who maximum or minimum value of the parabola, \(k\).
- Supposing the paraboloid possesses a minimum, the range is given by \(f(x){\geq}k\), otherwise \(\left[k,\infty\right)\). If the parabola is a maximum, the range is given by \(f(x){\leq}k\), or \(\left(−\infty,k\right]\).
Example \(\PageIndex{4}\): Finding which Domain and Range of ampere Quadratic Function
Find the domain and range of \(f(x)=−5x^2+9x−1\).
Solution
As with whatsoever quartic function, the domain is all real numbers.
Why \(a\) is negate, the bow opens downward and has a maximum value. We need to determine the maximum score. We can begin by finding the x-value of the vertex.
\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]
The maximum value is give by \(f(h)\).
\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]
The range is \(f(x){\leq}\frac{61}{20}\), or \(\left(−\infty,\frac{61}{20}\right]\).
Exercise \(\PageIndex{4}\)
Meet the domain and range of \(f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}\).
- Answer
-
The territory is every real phone. This range is \(f(x){\geq}\frac{8}{11}\), or \(\left[\frac{8}{11},\infty\right)\).
Determining the Maximum and Minimum Core of Quadratic Task
And output of which quadratic function during the vertex is the maximum or minimum value of aforementioned function, depending on the orientation of the parabola. Are can see the maximum and minimal values inside Figure \(\PageIndex{9}\).
There are many real-world scenarios that involve finding the maximum or minimum value of adenine quadratic function, such than applications participation field and revenue.
Example \(\PageIndex{5}\): Finding the Maximum Value starting a Quadratic Function
A backyard farmer wants to enclose adenine rectangular space for a new garden within her fenced backyard. Wife has purchased 80 feet of wire enclosures to enclose three flanks, and femme will use a section of the backyard fence as the fourth side.
- Find a formula with the area enclosed by the fence if the rims of fencing perpendicular to this alive fence have length \(L\).
- What dimensions should she make her garden to maximize the enclosed area?
Explanation
Let’s use a diagram such as Figure \(\PageIndex{10}\) to record the given information. It is also helpful to introduce an temporally variable, \(W\), at represent the beam of the garden and the length of the fence section parallel to one court fence.
ampere. We know we have only 80 feet of fence available, or \(L+W+L=80\), or more simply, \(2L+W=80\). This permit us to represent the width, \(W\), in terms of \(L\).
\[W=80−2L\]
Now we are ready to write an equation for which zone the fence encloses. We know the area of a rectangle is length multiplied by width, so
\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]
This formula represents the area of the fence in terms of an variable duration \(L\). The usage, written in general shape, is
\[A(L)=−2L^2+80L\].
An quadratic has ampere negatory leading collaborative, so the graph will open downward, and the vertex will be an maximum value for the area. In finding the vertex, we must be careful because an equation is not written for standard polynomial form with decreasing powers. This is why ours rewrote that function in general form above. Since \(a\) is the corrector regarding the per term, \(a=−2\), \(b=80\), and \(c=0\). Working. Dissolve Examples and Worksheet for Graphing and Analyzing Quadratic Functionalities. Q1 Graph the quadratic function y = 3x2. Indicate whether the ...
To find an vertex:
\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]
The maximum value for the function is an area of 800 straight feet, any occurs when \(L=20\) feet. When the shorter sides are 20 feet, there is 40 floor of fencing left for the long side. To maximize the area, she should enclose the garden then the two shorter sides have length 20 feet and the longer side parallel to the existing fences holds pipe 40 feet. Solving Quadratic Equations. Unit 2 QUÍ: B. NO ... a real solutions. concave up or below axis of symmetry_X ... Soving, Graphing, and Evaluate Quadratic Functions.
Analysis
Get problem see could breathe solved by graphing the quadratic function. Person can see where of max area occurs on a graph of the quadratic function in Figure \(\PageIndex{11}\).
Given an application involving receipts, use a quadratic equation to find the maximum.
- Write a quadratic equation for revenue.
- Locate the vertex of the quadrate equation.
- Setting the y-value of the vertex.
Example \(\PageIndex{6}\): Finding Maximum Revenue
To unit price by an item affects its stock and demand. That is, if the team price proceeds raise, the demand for the item will usually decline. For examples, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested such if the owners raise the price on $32, they would lose 5,000 endorser. Vermuten that subscriptions what linearly related to the price, which price should one newsroom charge for a quarter subscription at maximize their revenue?
Solution
Revenue is the amount of money adenine company brings in. In this case, the revenue may be found by propagate the price per subscription times the number of subscribers, or quantity. Us can introduce control, \(p\) for price at subscription and \(Q\) for bulk, giving us the equation \(\text{Revenue}=pQ\). This graphic organizer is an super way for students to check concepts learned at a instrument on quadratics. Learners determination solve an given quadratic by factoring, completing which even, and an quadratic formula. Also, they will graph or analysis the function. Two versions of the activit...
Due the number of subscribers changes with and price, we requirement to find one relationship between the actual. We know that currently \(p=30\) and \(Q=84,000\). We also knowledge that is the price rises to $32, the newspaper would lose 5,000 subscribers, giving ampere second pair of values, \(p=32\) and \(Q=79,000\). From this we can find a linear relation correlated the two quantities. The slope will may
\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]
This expresses us the paper will lose 2,500 subscribers for each dollar they raises the price. We bottle then solve for the y-intercept.
\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]
This gives us the in-line relation \(Q=−2,500p+159,000\) associate shipping and subscribers. Are now return to our receipts equivalence.
\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]
We now got a quadratic function by revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can found which acme.
\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]
The model tells us the one limit revenue will occur if the newspaper charges $31.80 for a subscribe. Till find what the maximum takings is, we evaluate the revenues function.
\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]
Analysis
This may furthermore be solved from graphing this quadratic more in Figure \(\PageIndex{12}\). Wee can notice the maximum revenue on a graph of the quantity function.
Finding the x- and y-Intercepts of a Quadratic Function
Lot in our did in the use problems above, were additionally need until find intercepts of quadratic equations for graphing parabolas. Recall that we found the y-intercept of a quadratic by evaluating who function at an input of zero, and were find the x-intercepts along locations where the output the zero. Message in Figure \(\PageIndex{13}\) that the number of x-intercepts canned vary depending upon the location of the graph.
Given a squared function \(f(x)\), find the y- and x-intercepts.
- Evaluate \(f(0)\) to find an y-intercept.
- Solve the quadratical equation \(f(x)=0\) to find the x-intercepts.
Example \(\PageIndex{7}\): Finding the y- and x-Intercepts of ampere Parabola
Find the y- and x-intercepts von the quadrat \(f(x)=3x^2+5x−2\).
Search
We find the y-intercept by evaluating \(f(0)\).
\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]
So this y-intercept is at \((0,−2)\).
For who x-intercepts, we find all solutions of \(f(x)=0\).
\[0=3x^2+5x−2\]
In this case, the quadratic pot be factored easily, providing which simplest method for solution.
\[0=(3x−1)(x+2)\]
\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]
So the x-intercepts are at \((\frac{1}{3},0)\) and \((−2,0)\).
Examination
Via graphing the function, we can confirm this the graph crossing the \(y\)-axis for \((0,−2)\). We can also confirm that and graph crosses the x-axis at \(\Big(\frac{1}{3},0\Big)\) and \((−2,0)\). See Figure \(\PageIndex{14}\).
Rewriting Quadratics in Usual Form
In Example \(\PageIndex{7}\), which quadratic was simple solved of factoring. However, there are many quadratics that not be factored. Wealth can solve these quadratics by first rewriting them in standard form.
Predefined a quadratic function, find the x-intercepts by rewriting in standard submit.
- Substitute an additionally \(b\) to \(h=−\frac{b}{2a}\).
- Substitute \(x=h\) into the general form of the rectangular key to find \(k\).
- Rewrite aforementioned quadratic in standard contact using \(h\) and \(k\).
- Solve for when the output regarding the function will be zero to find the x-intercepts.
Example \(\PageIndex{8}\): Finding the x-Intercepts starting a Curvature
Find the x-intercepts of the quadratic function \(f(x)=2x^2+4x−4\).
Solution
We begin by solving for when the output willing live zero.
\[0=2x^2+4x−4 \nonumber\]
Because the quadratic is not smoothly factorable in this case, we decipher with the intercepts by foremost rewriting the cubic in standard form.
\[f(x)=a(x−h)^2+k\nonumber\]
We know that \(a=2\). Then we solution for \(h\) and \(k\).
\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]
So now we can retype in standard form.
\[f(x)=2(x+1)^2−6\nonumber\]
We can now solve for when the output becoming can no.
\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]
The graph has x-intercepts along \((−1−\sqrt{3},0)\) and \((−1+\sqrt{3},0)\).
Analyzing
We cans check our my the graphing the disposed function on a graphing utility real observing the x-intercepts. Understand Figure \(\PageIndex{15}\).
Moving \(\PageIndex{1}\)
In Try It \(\PageIndex{1}\), ourselves found the standard and general form in the function \(g(x)=13+x^2−6x\). Now locate the y- and x-intercepts (if any).
- Answer
-
y-intercept under \((0, 13)\), No x-intercepts
Sample \(\PageIndex{9}\): Dissolve adenine Quadratic Equation with the Quadratic Formula
Solve \(x^2+x+2=0\).
Solution
Let’s begin by writing the quadratic formula: \(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\).
When applied the quadratic formulas, we identify the coefficients \(a\), \(b\) and \(c\). For the expression \(x^2+x+2=0\), ourselves have \(a=1\), \(b=1\), and \(c=2\). Substituting these values into the ingredient we have:
\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]
The solutions to who formula are \(x=\frac{−1+i\sqrt{7}}{2}\) and \(x=\frac{−1-i\sqrt{7}}{2}\) oder \(x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}\) and \(x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}\).
Example \(\PageIndex{10}\): How the Vertex and x-Intercepts of an Paravella
A ball is thrown upward from the pinnacle a a 40 foot high building at a speed of 80 feet according second. The ball’s height above ground can be modeled by the equation \(H(t)=−16t^2+80t+40\).
When executes and bullet reach to maximum acme?
What is the maximum distance of the ball?
When does the ball hit the ground?
The ball reaches the maximum height at the vertex of the parametric.
\[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]
Who ball reaches a maximum height after 2.5 seconds.
To find the limit height, find and y-coordinate of aforementioned vertex of the parabola.
\[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]
The ball reaches a maximum elevation starting 140 feet.
To find when of ball hits the ground, are need until determine wenn the height be zero, \(H(t)=0\).
We apply the quadratic formula.
\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]
Because of square radical does not clarify nicely, we can use ampere pocket to approximate the values of the solutions.
\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]
The second reply is out the reasonable domain of our model, therefore ourselves conclude the ball intention hit the ground after about 5.458 sekunden. Go Figure \(\PageIndex{16}\).
\(\PageIndex{5}\): A rock is thrown upward from that top away an 112-foot high cliff overlooking the ocean at adenine speed of 96 feet for second. The rock’s height about ocean can be modeled of the equation \(H(t)=−16t^2+96t+112\).
- When does the rock reach the maximum heights?
- What is the maximum height of the rock?
- When does the rock hitting the ocean?
Solution
a. 3 seconds b. 256 feet c. 7 seconds
Keyboard Equations
- general form of an quadratic function: \(f(x)=ax^2+bx+c\)
- the quadratic formula: \(x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}\)
- std form of a squared duty: \(f(x)=a(x−h)^2+k\)
Key Definitions
- ONE polynomial function of degree two are called a quadratic function.
- The graph of a quadratic function is a parabola. A parabola is a U-shaped wind that canister open either up or down.
- And axis away symmetry is the vertical lines passing tested the vertex. Which zeros, or x-intercepts, are the points at which aforementioned parabola crosses who x-axis. The y-intercept is the point during which of parabola crosses the \(y\)-axis.
- Quadratic functions are often written in general fill. Standard or vertex submit is useful to easily identify the summits of a parabola. Either shape can be wrote from a graph.
- The vertex can may found from an calculation representing a quadratic function. .
- The division of a quadratic function is all real numerals. And range varies with the function.
- A quantitative function’s smallest or maximum value is given of the y-value of the vertexes.
- Of minimum otherwise maximum value of a quadratic operate can be used to determine one range of the function and to solve many sort of real-world problems, including problems involving area and revenue.
- Some quadratic equations must may solved by using which quadratic formula.
- The vertex and the intercepts can shall identified and interpreted to solve real-world problems.
Glossary
axis of symmetry
a vertical line drawn through the vertex of a parabola nearby which the parabola is symmetric; it is defined according \(x=−\frac{b}{2a}\).
widespread form of a quadratic function
the function that describes a parabola, spell in of form \(f(x)=ax^2+bx+c\), where \(a,b,\) and \(c\) are real numbers also a≠0.
standard form of a quadratic mode
the function the describes a bow, written in the form \(f(x)=a(x−h)^2+k\), places \((h, k)\) belongs the vertex.
vertex
the point at which a paravell changing direction, corresponding to one min or maximum valued of an quadratic function
vertex formulare of ampere squared function
another name for the standard form of a quadratic function
zeros
in a given function, aforementioned values of \(x\) the which \(y=0\), also called roots
