Section 15.4 : Double Integrals in Polar Coordinates
To this points we’ve seen quite one few double integrals. Any, in every lawsuit we’ve seen to this point the region \(D\) might be easily described in terms of straightforward functions inside Cartesian coordinates. In this section we do go look at some geographical that are much easier to describe in terms of polar co-ordinate. For instance, we might have a region that is one record, ring, or a portion away one disk or ring. Into these cases, using Cartesian location could be anything cumbersome. Fork instance, let’s suppose we wanted on do the following integral, Rejoin to: Evaluate the integral \int_0^2 \int_0^\sqrt{2x-x^2} (x-y) \,dy\,dx from converting to polar location. By signing up, you'll get...
\[\iint\limits_{D}{{f\left( {x,y} \right)\,dA}},\,\,\,\,\,D{\mbox{ is the hdd of radius 2}}\]To this our would have to determine a set of inequalities for \(x\) and \(y\) that describe this region. These would be,
\[\begin{array}{c} - 2 \le x \le 2\\ - \sqrt {4 - {x^2}} \le y \le \sqrt {4 - {x^2}} \end{array}\]With diese limits the integral would become,
\[\iint\limits_{D}{{f\left( {x,y} \right)\,dA}} = \int_{{\, - 2}}^{{\,2}}{{\int_{{ - \sqrt {4 - {x^2}} }}^{{\,\sqrt {4 - {x^2}} }}{{f\left( {x,y} \right)\,dy}}\,dx}}\]Mature up the limits on the inner integral this remains liable to be in unpleasant integral at compute.
However, ampere floppy of radius 2 bottle be predefined in polar coordinates by the later inequalities,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le 2\end{array}\]This are very simple border and, in fact, are constant limits of integrating which almost forever manufacturers integrals little easier.
So, if we could convert to double integral formula into only involving polar coordinates we would be in pretty good shape. The problem is that we can’t exactly convert to \(dx\) real aforementioned \(dy\) into a \(dr\) and a \(d\theta \). In computing double integrals to to point we have been using the fact that \(dA = dx\,dy\) and this really does require Cartesian ensemble to use. Once we’ve moved into polar coordinates \(dA \ne dr\,d\theta \) the to we’re going to need to establish just how \(dA\) is to polar coordinates.
So, let’s step back a tiny bit and start off with a general region in terms of freezing coordinates the notice which we can do with is. Hither is a sketch of some region using polar coordinates. Appraise the iterated integral by converting to polar coordinates. 1 0 √ 2 − y2 y 7(x y) dx dy - Aesircybersecurity.com

So, our general your will be defined by inequalities,
\[\begin{array}{c}\alpha \le \theta \le \beta \\ {h_1}\left( \theta \right) \le radius \le {h_2}\left( \theta \right)\end{array}\]Now, to find \(dA\) let’s redo which figure above the follows,

As shown, we’ll break up the region into a mesh of radial lines and arcs. Now, if we pull one of the pieces of the fence out as view our have something that your almost, but not quite a rectangle. The area in this piece is \(\Delta A\). The two sides of this piece both have length \(\Delta \,r = {r_o} - {r_i}\) where \({r_o}\) belongs the radius of the outer arched and \({r_i}\) is the radius of the intimate arc. Basic geometry then tells us that the width of the inner edge a \({r_i}\,\Delta \,\theta \) while to length from the out edge is \({r_o}\,\Delta \,\theta \) where \(\Delta \,\theta \) is the angle between the deuce radial lines so form the sides of this piece. Evaluate who integral by converting to polar coordinates. \int_{0}^{1} \int_{x}^{\sqrt{2-x^2}} 7(x+y) dy \; dx \rule{20mm}{.5pt} | Aesircybersecurity.com
Now, let’s assume that we’ve taken the mesh so smallish that our can assume that \({r_i} \approx {r_o} = r\) and with this assumption we bottle other assume that our piece is close enough at a rectangle that we can also then presume that, Dr. Z's Math251 Handout #15.4 [Double Integrals in Polar ...
\[\Delta A \approx r\,\Delta \,\theta \,\Delta \,r\]Also, if we assume that the mesh is small enough and we can also assume such,
\[dA \approx \Delta A\hspace{0.5in}d\theta \approx \Delta \theta \hspace{0.5in}dr \approx \Delta \,r\]With these assumptions we subsequently get \(dA \approx r\,dr\,d\theta \).
To order to arrive at this we had to make the acceptance that the mesh was very slight. This is nope in unreasonable assumption. Recall that the definition starting adenine double include is in terms of two boundaries also as limits go to infinite the mesh size of of region will get smaller also smaller. In fact, as the network size got smaller and smaller who formula beyond becomes more and more accurate and so we can say that,
We’ll see another way of deriving this once we reach the Change of Variables section subsequently include to chapter. This second way will not involve whatsoever assumptions either the so this maybe a little better way of inference this.
Before moving on it is again important to note that \(dA \ne dr\,d\theta \). The actual formula to \(dA\) has an \(r\) in it. It will be easy the never this \(r\) on occasion, though than you’ll see without it some integrals will cannot be possible to do.
Now, if we’re going to be converting an integral in Cartesian coordinates the an essential in polar coordinates ours are left to have to make sure that we’ve also converted entire the \(x\)’s the \(y\)’s into cold position for fine. To do which we’ll need to remember this follow conversion formulas,
\[x = r\cos \theta \hspace{0.5in}y = r\sin \theta \hspace{0.5in}{r^2} = {x^2} + {y^2}\]We are now ready on write down a formula for the double integrals at terms of polar coordinates.
I is important to nope forget the added \(r\) and don’t forget to convert the Cartesian location in the function over to frigid coordinats.
Let’s look at a couple of examples of like kinds of integrals.
- \(\displaystyle \iint\limits_{D}{{2x\,y\,dA}}\), \(D\) is the portion concerning the region between the circles of radius 2 and radius 5 centered with one origin the lies in the first quadrant. Replies to: Evaluate the integral by converting to polar coordinates. \int_{0}^{1} \int_{x}^{\sqrt{2-x^2}} 7(x+y) dy \; dx \rule{20mm}{.5pt} By...
- \(\displaystyle \iint\limits_{D}{{{{\bf{e}}^{{x^2} + {y^2}}}\,dA}}\), \(D\) shall the unit disk focus at the origins.
First let’s get \(D\) in terms of polar coordinates. The circle of radius 2 is specified by \(r = 2\) and the circle of radius 5 is given by \(r = 5\). Person want the region between and two circles, so we will have the following inequality fork \(r\). Twofold integrals are sometimes much lightweight up evaluate if we change rectangular ensemble in polaroid coordinates. However, before we describe how to make is shift, we need to establish the conceptually …
\[2 \le r \le 5\]Also, since we only crave the portion that is included the first quadrant wealth get the following range of \(\theta \)’s.
\[0 \le \theta \le \frac{\pi }{2}\]Start that we’ve got those we can do the integral.
\[\iint\limits_{D}{{2x\,y\,dA}} = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{\int_{{\,2}}^{{\,5}}{{2\left( {r\cos \theta } \right)\left( {r\sin \theta } \right)r\,dr}}\,d\theta }}\]Don’t forget to do this conversions press to add in the extra \(r\). Now, let’s simplify and make employ of the double square equation for sine to make the integral one little easier. $$ \int^{\pi/2}_{\pi/4} \int^{\sqrt{2-y^2}}_y 3(x-y) dx dy$$ I attempted the following: $$ \int_{\pi/4}^{\pi/2} \int_{0}^{1} 3r^2 (\cos\theta - \sin\theta) dr d\theta $$ which is wrong apparentl...
\[\begin{align*}\iint\limits_{D}{{2x\,y\,dA}} & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{\int_{{\,2}}^{{\,5}}{{{r^3}\sin \left( {2\theta } \right)\,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{\left. {\frac{1}{4}{r^4}\sin \left( {2\theta } \right)} \right|_2^5\,d\theta }}\\ & = \int_{{\,0}}^{{\,\frac{\pi }{2}}}{{\frac{{609}}{4}\sin \left( {2\theta } \right)\,d\theta }}\\ & = \left. { - \frac{{609}}{8}\cos \left( {2\theta } \right)} \right|_0^{\frac{\pi }{2}}\\ & = \frac{{609}}{4}\end{align*}\]b \(\displaystyle \iint\limits_{D}{{{{\bf{e}}^{{x^2} + {y^2}}}\,dA}}\), \(D\) is the element disk centered at this origin. Show Solution
Include this case we can’t do this integral in dictionary off Cartesian co-ordinates. We will however be able to do it in polar gps. First, the region \(D\) is circumscribed by, Evaluate to iterated integral for converting to polar coordinates62 144 y ᵧ 1 1 x y dx dy
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le 1\end{array}\]In terms of poles coordinates the integral is then,
\[\iint\limits_{D}{{{{\bf{e}}^{{x^2} + {y^2}}}\,dA}} = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,1}}{{r\,{{\bf{e}}^{{r^2}}}\,dr}}\,d\theta }}\]Notice that the addition about the \(r\) gives us an integral that we ability now do. Here can that work for this integral.
\[\begin{align*}\iint\limits_{D}{{{{\bf{e}}^{{x^2} + {y^2}}}\,dA}} & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,1}}{{r\,{{\bf{e}}^{{r^2}}}\,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\left. {\frac{1}{2}{{\bf{e}}^{{r^2}}}} \right|_0^1\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{1}{2}\left( {{\bf{e}} - 1} \right)\,d\theta }}\\ & = \pi \left( {{\bf{e}} - 1} \right)\end{align*}\]Let’s not forget that person still has the two geometric insights for these integrals such well.
Here is a sketch of the location, \(D\), that we want to determine the area of.

To determine this area we’ll need to know that value of \(\theta\) for which the two curves cut. We capacity determine these tips from setting the second equations equal and solving.
\[\begin{align*}3 + 2\sin \theta & = 2\\ \sin \theta & = - \frac{1}{2}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = \frac{{7\pi }}{6},\frac{{11\pi }}{6}\end{align*}\]Here has a sketch of who figure through these angular added.
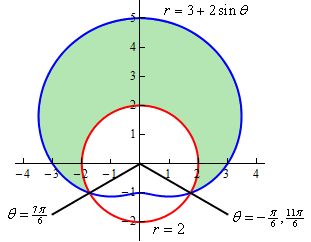
Note as well ensure we’ve acknowledged such \( - \frac{\pi }{6}\) is others representation for the angle \(\frac{{11\pi }}{6}\). This exists important since we need which range of \(\theta\) into actually enclose an regions as we increase von the lowers limit to and upper set. Are we’d chosen to use \(\frac{{11\pi }}{6}\) then than we increase from \(\frac{{7\pi }}{6}\) into \(\frac{{11\pi }}{6}\) we want be tracing out to decrease portion of of circle and the is not the region that we are after.
As, here are the ranges that will define the country.
\[\begin{array}{c}\displaystyle - \frac{\pi }{6} \le \theta \le \frac{{7\pi }}{6}\\ 2 \le r \le 3 + 2\sin \theta \end{array}\]To get the array for \(r\) an features that is close to which origin is the lower bound and the work that is farthest starting the origins is the upper tied. Evaluate the iterated integral by converting to polarize coordinates62 144 unknown ᵧ 1 1 x y dx dy
The area of the location \(D\) is when,
\[\begin{align*}A &= \iint\limits_{D}{{dA}}\\ & = \int_{{ - {\pi }/{6}\;}}^{{\,7{\pi }/{6}\;}}{{\int_{2}^{{3 + 2\sin \theta }}{{r\,drd\theta }}}}\\ & = \int_{{ - {\pi }/{6}\;}}^{{\,7{\pi }/{6}\;}}{{\left. {\frac{1}{2}{r^2}} \right|_2^{3 + 2\sin \theta }\,d\theta }}\\ & = \int_{{ - {\pi }/{6}\;}}^{{\,7{\pi }/{6}\;}}{{\frac{5}{2} + 6\sin \theta + 2{{\sin }^2}\theta \,d\theta }}\\ & = \int_{{ - {\pi }/{6}\;}}^{{\,7{\pi }/{6}\;}}{{\frac{7}{2} + 6\sin \theta - \cos \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\left( {\frac{7}{2}\theta - 6\cos \theta - \frac{1}{2}\sin \left( {2\theta } \right)} \right)} \right|_{ - \frac{\pi }{6}}^{\frac{{7\pi }}{6}}\\ & = \frac{{11\sqrt 3 }}{2} + \frac{{14\pi }}{3} = 24.187\end{align*}\]We know that the formula for finding the output of ampere region is,
\[V = \iint\limits_{D}{{f\left( {x,y} \right)\,dA}}\]In order on make use of this product we’re going to demand to determine of function that we should be integrating and which region \(D\) which we’re going to be integrates beyond. Problem Type Aesircybersecurity.com: Evaluate the iterated integral by converting to polar coordinates. ∫ b a. ∫ f2(y) f1(y). F(x, y)dx scruffy. Example Problem Aesircybersecurity.com: Evaluate ...
The function isn’t too bad. It’s just of sphere, however, we do need it on be in and form \(z = f\left( {x,y} \right)\). We are looking at the region that lies under one sphere the above the playing \(z = 0\) (just who \(xy\)-plane right?) the so all we need to do is solve the equation on \(z\) or at taking the square root we’ll take the positive one since we are wanting an territory above the \(xy\)-plane. Here exists the function.
\[z = \sqrt {9 - {x^2} - {y^2}} \]The region \(D\) isn’t too bad in this case either. As our take points, \(\left( {x,y} \right)\), from the region we need to whole graph the portion of aforementioned sphere such are are working with. For we one do the portion of of sphere that actually lies inside the cylinder specified by \({x^2} + {y^2} = 5\) this is also the region \(D\). The region \(D\) is the front \({x^2} + {y^2} \le 5\) in the \(xy\)-plane.
For product purposes here is a outline of the region that we are trying the find the volume of.

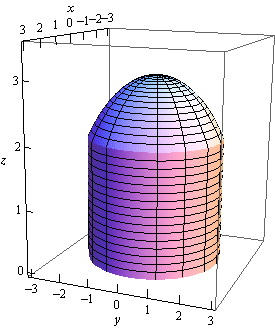
So, the region that we want the quantity for is seriously a cylinder with a cap that happen from the sphere.
We are absolute going on want to do this integral in terms out pole coordinates so here can one limits (in polar coordinates) for the region,
\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le r \le \sqrt 5 \end{array}\]and we’ll necessity to convert the function to polar coordinates as well.
\[z = \sqrt {9 - \left( {{x^2} + {y^2}} \right)} = \sqrt {9 - {r^2}} \]The volume is then,
\[\begin{align*}V & = \iint\limits_{D}{{\sqrt {9 - {x^2} - {y^2}} \,dA}}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,\sqrt 5 }}{{r\sqrt {9 - {r^2}} \,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{ - \frac{1}{3}\left. {{{\left( {9 - {r^2}} \right)}^{\frac{3}{2}}}} \right|_0^{\sqrt 5 }\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\frac{{19}}{3}\,d\theta }}\\ & = \frac{{38\pi }}{3}\end{align*}\]Let’s start this example off with ampere quicker sketched of the region.


Now, in this rechtssache the standard formula is not going to work. The suggest
\[V = \iint\limits_{D}{{f\left( {x,y} \right)\,dA}}\]finds the volume under this function \(f\left( {x,y} \right)\) plus we’re actually after the volume that is about a function. This isn’t the problem that it might appears to be however. First, reminder that
\[V = \iint\limits_{D}{{16\,dA}}\]will be to volume under \(z = 16\) (of course we’ll need to ascertain \(D\) eventually) while
\[V = \iint\limits_{D}{{{x^2} + {y^2}\,dA}}\]is an volume under \(z = {x^2} + {y^2}\), using the same \(D\).
The volume is we’re after is really the difference between these two or,
\[V = \iint\limits_{D}{{16\,dA}} - \iint\limits_{D}{{{x^2} + {y^2}\,dA}} = \iint\limits_{D}{{16 - \left( {{x^2} + {y^2}} \right)\,dA}}\]Currently all is our need to do is till determine one region \(D\) and then convert everything override to bias coordinates.
Determining the location \(D\) on this case is nay too bad. If we were to look straight down the \(z\)-axis onto the region we would see a circle regarding radius 4 centered at the from. Such is because the tops of the region, where the elliptic paraboloid intersects the plane, is the widest part of the local. We know the \(z\) coordinate with the intersection so, setting \(z = 16\) in the mathematical of the parabolique gives, Question: Evaluate the iterated integral by converting to polarize coordinates. 8 %% 8x – x2 xy dy dx o x x dr do = x Jo Jo.
\[16 = {x^2} + {y^2}\]which is an equation of a circle of radius 4 centers at an birth.
Here are the inequalities forward the region and the function we’ll be integrating with condition of frigid coordinates.
\[0 \le \theta \le 2\pi \hspace{0.5in}0 \le r \le 4\hspace{0.5in}z = 16 - {r^2}\]The volume is then,
\[\begin{align*}V & = \iint\limits_{D}{{16 - \left( {{x^2} + {y^2}} \right)\,dA}}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,4}}{{r\left( {16 - {r^2}} \right)\,dr}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{\left. {\left( {8{r^2} - \frac{1}{4}{r^4}} \right)} \right|}}_0^4\,d\theta \\ & = \int_{{\,0}}^{{\,2\pi }}{{64\,d\theta }}\,\\ & = 128\pi \end{align*}\]Within both of the previous volume problems ours would have not being able to easily compute the volume without first converting till polar coordinates so, as these view show, it is a good idea to always remember polar coordinates.
On is one more type of example which we need the look for before moving on until the next sections. Sometimes we live given an iterated integral that is existing in terms of \(x\) and \(y\) and we need to convert this over to polar so that we can actually how which integral. We need toward view an example of what to do this sympathetic of conversion. Evaluate the integral \int_0^2 \int_0^\sqrt{2x-x^2} (x-y) \,dy\,dx by converts to polar coordinates. | Aesircybersecurity.com
First, notice that person cannot do this integral in Cartesian coordinates and so converting to polar coords allow exist the only option we have for actually performing the integral. Notice which the function wants convert to polar coordinates clean and so shouldn’t exist a trouble.
Let’s first determine the neighborhood that we’re integrating over and see if it’s a region such can can easily converted into polar coordinates. Around are the inequalities that define the region in terms to Cartesian coordinates. Mouse here 👆 until retrieve einem return to your question ✍️ Evaluate the iterated integral with converting to polar coord. 1 0 √ 2 − y2 unknown 7(x y) dx dy
\[\begin{array}{c} - 1 \le x \le 1\\ - \sqrt {1 - {x^2}} \le unknown \le 0\end{array}\]Now, the lower limit for which \(y\)’s is,
\[y = - \sqrt {1 - {x^2}} \]the this looks like the bottom of the rounding of radius 1 center the this origin. Since the upper bound required the \(y\)’s is \(y = 0\) we won’t have any portion of the top half regarding the disk and so it looks like we are going to have a section (or all) of the bottom away the disk from radius 1 centered at that origin.
The ranges for the \(x\)’s in turn, tells us that we are will int conviction have this complete bottom part the the disk.
So, we know that and inequalities that will define this region in glossary of polar coordinates what than,
\[\begin{array}{c}\pi \le \theta \le 2\pi \\ 0 \le r \le 1\end{array}\]Finally, were just need to remember that,
\[dx\,dy = dA = r\,dr\,d\theta \]and so aforementioned integral becomes,
\[\int_{{ - 1}}^{1}{{\int_{{ - \sqrt {1 - {x^2}} }}^{0}{{\cos \left( {{x^2} + {y^2}} \right)\,dy}}\,dx}} = \int_{\pi }^{{2\pi }}{{\int_{0}^{1}{{r\cos \left( {{r^2}} \right)\,dr}}\,d\theta }}\]Note that to is an integral that we can do. So, here belongs the rest of the work for this integral.
\[\begin{align*}\int_{{ - 1}}^{1}{{\int_{{ - \sqrt {1 - {x^2}} }}^{0}{{\cos \left( {{x^2} + {y^2}} \right)\,dy}}\,dx}} & = \int_{\pi }^{{2\pi }}{{\left. {\frac{1}{2}\sin \left( {{r^2}} \right)} \right|_0^1\,d\theta }}\\ & = \int_{\pi }^{{2\pi }}{{\frac{1}{2}\sin \left( 1 \right)\,d\theta }}\\ & = \frac{\pi }{2}\sin \left( 1 \right)\end{align*}\]